原神暴击率有什么用 暴击作用及暴击爆伤黄金比例详解

原神游戏中旅行者在升级角色的时候暴击会提升，但是很多的玩家并不太懂暴击的作用和伤害计算，因此小编今天来为大家总结一下关于暴击的各个问题解答，相信玩家在看完之后就能够合理的对角色进行搭配了；

原神暴击作用及暴击爆伤黄金比例详解

【实用结论一览】

①【暴击时伤害】=【未暴击伤害】*（1+面板暴伤）

②【伤害期望】=未暴击伤害*（1+暴率*暴伤）

对比哪套暴击面板好，只需要对比暴率和暴伤的乘积即可！

③宗室武器你本身暴率越高，武器被动越没用

本身暴率到50%以后，被动可以看成+6%暴率，仅此而已

④保持面板暴率：暴伤=1:2收益最高

（甘雨被动这类可以直接算进“面板暴率”）

⑤一般先把面板攻击力堆到绿字/白字=120%，然后开始堆暴击属性即可

Part 1 【暴击时伤害是怎么计算的】

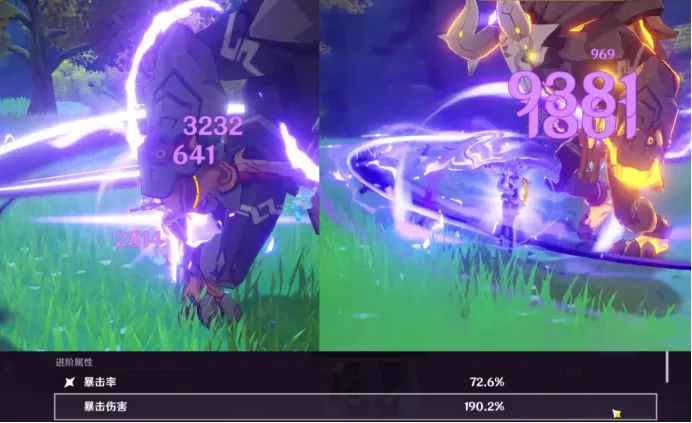
用图中下方的暴击面板进行测试，未暴击伤害为3232，暴击时伤害为9381

可以发现，3232*（1+190.2%）=9379→9381

误差来源于暴伤面板隐藏的第二位小数。

也就是说，【暴击时伤害】=【未暴击伤害】*（1+面板暴伤）

很简单的式子，唯一需要注意的就是这个“1”别忘了加上去

Part 2 【什么是“伤害期望”】

还是先通过一个实际问题展开：

【第一组】

凝光使用图中的面板，暴击45.4%，暴伤160.4%，接下里我将会用芭芭拉打晕火树，然后凝光使用EQE连招，不做其它动作，测试伤害

天权崩玉启动

EQE结束，记录此时火树的血条，过会和下一组测试的对比

【第二组】

第二组，暴击面板换成67.2%/119.1%，同样用芭芭拉破盾，凝光仅使用EQE测试伤害

EQE启动，可以注意到火树的名字变成了“摇曳的炽焰火花”，名字的变动正好有利于我们标记“第二组”

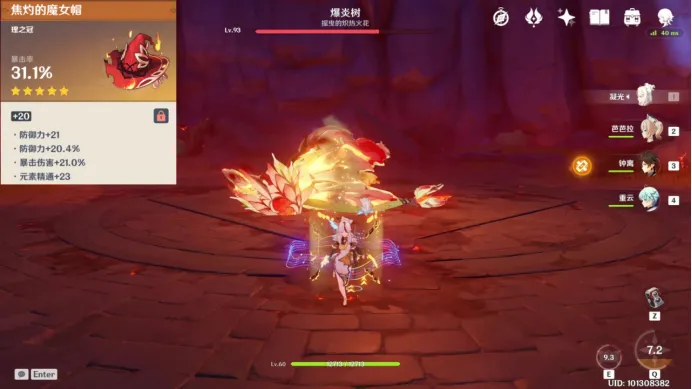
好，测试结束，记住45/160的面板所测试火树叫“恒常燃烧的巨藤”，67/119的面板对应“摇曳的炽焰火花”

造成的伤害直接用boss血条的变化来进行直观展示，显然，67/119的面板最后造成了更高的伤害。

决定总体伤害高低的不是“暴击伤害”而是“平均伤害”，这和暴击几率密切相关，是个概率统计问题，但并不复杂。

引入概念“伤害期望”其实就是使用某个暴击面板所造成伤害的【数学期望】

得到E=D（1-p）+D（1+q）p=D（1+pq）

即【伤害期望】=未暴击伤害*（1+暴率*暴伤）

伤害期望便是衡量这套面板输出能力的标准，根据公式，可以得到一个实用的结论：

--对比哪套暴击面板好，只需要对比暴率和暴伤的乘积即可！--

比如刚才例子中的45/160和67/119

进行对比只需要：

E1=0.45*1.6=0.7200

E2=0.67*1.19=0.7973

E2＞E1

所以第二套的伤害期望更高，事实也确实如此。

Part 3 【为什么暴率暴伤1:2最佳】

首先，在游戏内我们可以发现，暴率、攻击、暴伤符合1:1.5:2的比例出现，也就是说，1%暴率和2%暴伤的“分量”是相同的。

习惯上，定义1%暴率所占的“分量”叫做“单位权重”，单位权重和各词条属性的关系通过20级圣遗物主词条数值除以31.1就可以得到：

1单位权重=1%暴率=1.15%治疗加成=1.5%攻击加成=1.5%元素增伤=1.67%充能效率=1.875%物伤加成=1.875%防御加成=2%暴伤=6元素精通

我们给暴率和暴伤设定一个总权重M，这代表圣遗物的双暴质量

对于质量相同的圣遗物，可以得到2p（暴率）+q（暴伤）=2M

由均值不等式，

当且仅当p：q=1:2时取等

所以同样成本下，暴率：暴伤=1:2时，伤害最高

Part 4 【宗室系列武器收益如何】

对于这个问题，我们做个比喻：

Q：某活动中奖的概率是20%，如果这次没中奖，下次中奖的概率提升8%，最多提升5次，加40%。中奖后概率从20%重新计算。

问：综合中奖率是多少？

解决这个问题的关键在于，要把“中奖率”看成常数x1、x2、x3，然后去计算P（x=x1）这样的概率，把“期望概率”求出来，不然问题会变得非常复杂。

比如，“第二次才中奖的概率”就是（1-20%）*（20%+8%）=22.4%，那么P（x=x2）就是22.4%，以此类推，得到下表：

注意最后一栏的p是1减去前面得到的五个概率值

所谓综合中奖率就是：

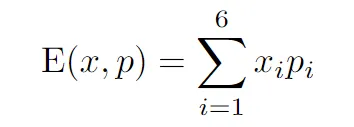
≈37.15%

这个模型里的“初始中奖率”是20%，根据原神的实际情况，暴率应该从5%到100%不断变化，由刚才的方法，可以绘制出【当暴率为p时，装备宗室系列武器后的“等效面板暴率”】曲线：

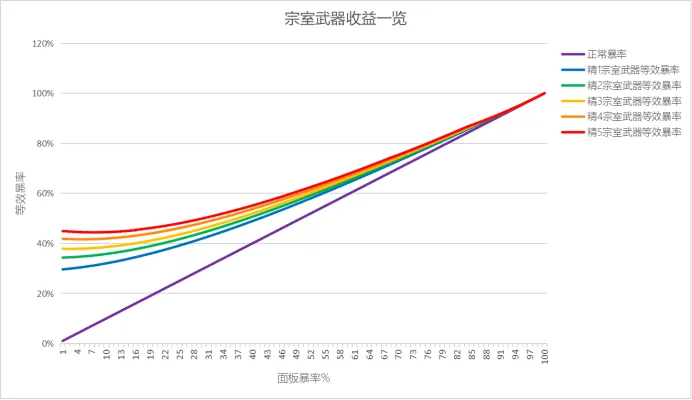
总结，

你本身的暴率达到50%以后，这把武器的收益就已经很低了，仅相当于提供6%以下的面板暴率，所以……真没啥用= =

Part 5 【暴击属性对于角色的收益情况】

收益公式的推导可以参考攻击力、暴击边际收益曲线

攻击力、暴击属性收益曲线

就用可莉的收益曲线来举例，图中蓝色曲线即为暴击收益曲线

【分段的含义：】

①由于基础面板是5/25，所以一开始只堆暴率，每个单位1%，直到面板达到25/50

②同步提升暴率和暴伤，每个单位（0.5%暴率+1%暴伤），直到满暴100/200

③满暴后只堆暴伤，每个单位2%

【从中得到的结论】

①“暴击不会稀释”的说法是错误的

②相比攻击收益，暴击属性在后期发力，一般先把攻击绿字/白字堆到120%即停手，转堆暴击。

Part 6【“实际暴击次数所占比例≠面板暴率”带来的启发】

一个流程中的暴击次数满足二项分布特点。

设暴率为p

攻击次数n

暴击次数k

攻击n次中暴击k次的概率为：

涉及到的变量有n、p、k，式子中又有组合数以及求和符号，比较复杂。为了得出结论，只好挑选几种具有代表性的特殊情况来进行分析。

令n=100；500；1000

而p=50%不变

也就是研究在100、500/1000次攻击时，50%面板暴率下，实际暴击次数的分布情况

Exl  公式如图↑

然后作出图像↓

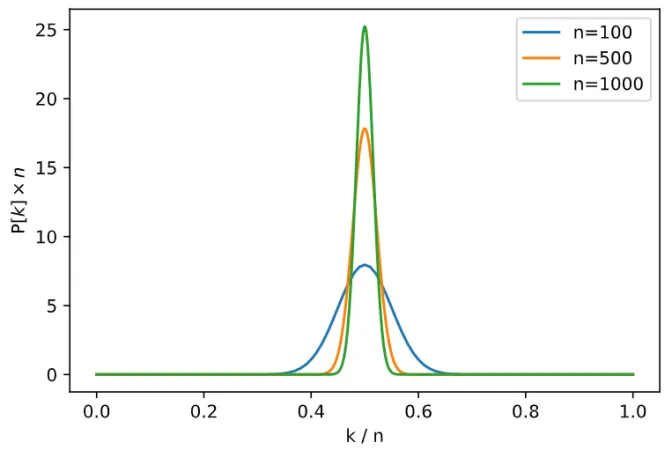
①这是典型的正态分布规律，中间高两边低，峰值出现在面板暴率处。

②攻击次数越高，伤害越接近期望值，可能会有正负差，但过大差值几乎不可能出现。

③100到1000图像形态的“变宽”、“变高”意味着，攻击次数越低，我们就越有可能打出超越面板暴率的实际效果。

如果我们把n降到30，制作此时的暴击分布示意图

好了，可以看到，在x=15的两边，频数的分布都很高，而且范围不小。这是一个好消息——通过凹挑战次数，我们完全可以用50%的面板打出60%面板的效果，甚至更高。

具体如何呢？

一般来说，一关凹10次也不高兴继续凹了

看图像的面积，如果能截出面积大于0.1的一部分来，就是10%凹成功率对应的实际效果暴率。而图中对应的就是x=19-23的部分，总面积达到约0.1

什么意思呢？

此时你有10%的概率用50%的暴率面板打出65%暴率的伤害期望

并且，如果我们仍然令n=30，但p取不同的值，绘制图像：

可以发现，几个图像没有明显的区别，那就可以近似得认为，30次攻击的流程里，有10%的概率将你的实际暴击凹到（面板暴率+15%）！

但实际操作中，攻击次数实在难以量化，改变配队思路来提高伤害比凹暴率更加明智，这些研究只能作为一种思路上的启发，了解即可，个人感觉使用价值非常有限……